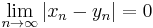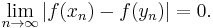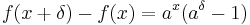Uniform continuity
In mathematics, a function ƒ is uniformly continuous if, roughly speaking, it is possible to guarantee that ƒ(x) and ƒ(y) be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between ƒ(x) and ƒ(y) cannot depend on x and y themselves. For instance, any isometry (distance-preserving map) between metric spaces is uniformly continuous.
Every uniformly continuous function between metric spaces is continuous. Uniform continuity, unlike continuity, relies on the ability to compare the sizes of neighbourhoods of distinct points of a given space. In an arbitrary topological space this may not be possible. Instead, uniform continuity can be defined on a metric space where such comparisons are possible, or more generally on a uniform space.
The equicontinuity of a set of functions is a generalization of the concept of uniform continuity.
Contents |
Definition for functions on metric spaces
Given metric spaces (X, d1) and (Y, d2), a function ƒ : X → Y is called uniformly continuous if for every real number ε > 0 there exists δ > 0 such that for every x, y ∈ X with d1(x, y) < δ, we have that d2(ƒ(x), ƒ(y)) < ε.
If X and Y are subsets of the real numbers, d1 and d2 can be the standard Euclidean norm, | · |, yielding the definition: for all ε > 0 there exists a δ > 0 such that for all x, y ∈ X, |x − y| < δ implies |ƒ(x) − ƒ(y)| < ε.
The difference between being uniformly continuous, and simply being continuous at every point, is that in uniform continuity the value of δ depends only on ε and not on the point in the domain.
Local versus global
Continuity itself is a local (more precisely, pointwise) property of a function—that is, a function f is continuous, or not, at a particular point. When we speak of a function being continuous on an interval, we mean only that it is continuous at each point of the interval. In contrast, uniform continuity is a global property of f, in the sense that the standard definition refers to pairs of points rather than individual points. On the other hand, it is possible to give a local definition in terms of the natural extension f*, see below.
Examples and properties
- Every Lipschitz continuous map between two metric spaces is uniformly continuous. In particular, every function which is differentiable and has bounded derivative is uniformly continuous. More generally, every Holder continuous function is uniformly continuous.
- Every member of a uniformly equicontinuous set of functions is uniformly continuous.
- The tangent function is continuous on the interval (−π/2, π/2) but is not uniformly continuous on that interval.
- The exponential function x
 ex is continuous everywhere on the real line but is not uniformly continuous on the line.
ex is continuous everywhere on the real line but is not uniformly continuous on the line.
Properties
- It is an immediate consequence of the definitions that every uniformly continuous function is continuous.
- The converse does not hold. Consider for instance the function
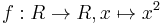 . Let
. Let 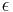 be any positive real number. Then uniform continuity requires the existence of a positive number
be any positive real number. Then uniform continuity requires the existence of a positive number  such that for all
such that for all 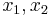 with
with 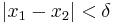 , we have
, we have 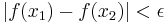 . But for any positive number
. But for any positive number  , we have
, we have  , and for all sufficiently large x this quantity is greater than
, and for all sufficiently large x this quantity is greater than  .
.
- If
 ,
,  is uniformly continuous and
is uniformly continuous and  is bounded, then
is bounded, then  is a bounded subset of R. In particular, the function
is a bounded subset of R. In particular, the function 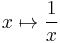 from (0,1) to R is continuous but not uniformly continuous.
from (0,1) to R is continuous but not uniformly continuous.
- More generally, the image of a totally bounded subset under a uniformly continuous function is totally bounded. Beware that the image of a bounded subset of an arbitrary metric space under a uniformly continuous function need not be bounded. For instance, consider the identity function from the integers endowed with the discrete metric to the integers endowed with the usual Euclidean metric.
- The Heine-Cantor theorem asserts that if X is compact, then every continuous f : X → Y is uniformly continuous. In particular, if a function is continuous on a closed bounded interval of the real line, it is uniformly continuous on that interval. The Darboux integrability of continuous functions follows almost immediately from the uniform continuity theorem.
- If a real-valued function
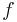 is continuous on
is continuous on  and
and  exists (and is finite), then
exists (and is finite), then 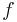 is uniformly continuous. In particular, every element of
is uniformly continuous. In particular, every element of 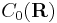 , the space of continuous functions on R that vanish at infinity, is uniformly continuous. Note that this is a generalization of the Heine-Cantor theorem mentioned above, since
, the space of continuous functions on R that vanish at infinity, is uniformly continuous. Note that this is a generalization of the Heine-Cantor theorem mentioned above, since 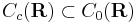 .
.
Other characterisations
Non-standard analysis
In non-standard analysis, a real-valued function ƒ of a real variable is continuous at a point a precisely if the difference ƒ(a + δ) − ƒ(a) is infinitesimal whenever δ is infinitesimal. Thus ƒ is continuous on a set A in R precisely if such a property is satisfied at every real point a ∈ A. Uniform continuity can be expressed as the condition that the same is true not only at real points in A, but at all points in its non-standard counterpart (natural extension) *A in *R.
If A has any infinite bounded subset, then *A contains points differing by infinitely small amounts from real points in A. If A is unbounded, then *A contains infinitely large non-standard real numbers.
Example 1. The trigonometric tangent function, continuous on the open interval (−π/2, π/2) fails to be uniformly continuous on that set because there are infinitely small positive real numbers δ such that tan(π/2 − δ) and tan(π/2 − 2δ) differ by more than an infinitely small amount.
Example 2. The exponential function exp, continuous on the real line R, fails to be uniformly continuous on R because there are infinitely large non-standard real numbers x and infinitely small non-standard real numbers δ such that exp(x + δ) − exp(x) is not infinitely small. A more explicit calculation in the case of the squaring function x2 appears at Non-standard calculus.
Characterization via sequences
For a function between Euclidean spaces, uniform continuity can defined in terms of how the function behaves on sequences (Fitzpatrick 2006). More specifically, let A be a subset of Rn. A function ƒ : A → Rm is uniformly continuous if and only if for every pair of sequences xn and yn such that
we have
Relations with the extension problem
Let X be a metric space, S a subset of X, and 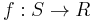 a continuous function. When can f be extended to a continuous function on all of X?
a continuous function. When can f be extended to a continuous function on all of X?
If S is closed in X, the answer is given by the Tietze extension theorem: always. So it is necessary and sufficient to extend f to the closure of S in X: that is, we may assume without loss of generality that S is dense in X, and this has the further pleasant consequence that if the extension exists, it is unique.
Let us suppose moreover that X is complete, so that X is the completion of S. Then a continuous function 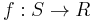 extends to all of X if and only if f is Cauchy-continuous, i. e., the image under f of a Cauchy sequence remains Cauchy. (In general, Cauchy continuity is necessary and sufficient for extension of f to the completion of X, so is a priori stronger than extendability to X.)
extends to all of X if and only if f is Cauchy-continuous, i. e., the image under f of a Cauchy sequence remains Cauchy. (In general, Cauchy continuity is necessary and sufficient for extension of f to the completion of X, so is a priori stronger than extendability to X.)
It is easy to see that every uniformly continuous function is Cauchy-continuous and thus extends to X. However, for functions defined on unbounded spaces like R, uniform continuity is a rather strong condition, and it is desirable to have a weaker condition from which to deduce extendability.
For example, suppose a > 1 is a real number. At the precalculus level, the function 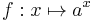 can be given a precise definition only for rational values of x (assuming the existence of qth roots of positive real numbers, an application of the Intermediate Value Theorem). One would like to extend f to a function defined on all of R. The identity
can be given a precise definition only for rational values of x (assuming the existence of qth roots of positive real numbers, an application of the Intermediate Value Theorem). One would like to extend f to a function defined on all of R. The identity
shows that f is not uniformly continuous on all of Q; however for any bounded interval I the restriction of f to 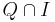 is uniformly continuous, hence Cauchy-continuous, hence f extends to a continuous function on I. But since this holds for every I, there is then a unique extension of f to a continuous function on all of R.
is uniformly continuous, hence Cauchy-continuous, hence f extends to a continuous function on I. But since this holds for every I, there is then a unique extension of f to a continuous function on all of R.
More generally, a continuous function 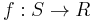 whose restriction to every bounded subset of S is uniformly continuous is extendable to X, and the converse holds if X is locally compact.
whose restriction to every bounded subset of S is uniformly continuous is extendable to X, and the converse holds if X is locally compact.
A typical application of the extendability of a uniform continuous function is the proof of the inverse Fourier transformation formula. We first prove that the formula is true for test functions, there are densely many of them. We then extend the inverse map to the whole space using the fact that linear map is continuous; thus, uniformly continuous.
Generalization to topological vector spaces
In the special case of two topological vector spaces 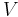 and
and 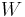 , the notion of uniform continuity of a map
, the notion of uniform continuity of a map  becomes : for any neighborhood
becomes : for any neighborhood  of zero in
of zero in 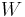 , there exists a neighborhood
, there exists a neighborhood  of zero in
of zero in 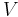 such that
such that  implies
implies 
For linear transformations  , uniform continuity is equivalent to continuity. This fact is frequently used implicitly in functional analysis to extend a linear map off a dense subspace of a Banach space.
, uniform continuity is equivalent to continuity. This fact is frequently used implicitly in functional analysis to extend a linear map off a dense subspace of a Banach space.
Generalization to uniform spaces
Just as the most natural and general setting for continuity is topological spaces, the most natural and general setting for the study of uniform continuity are the uniform spaces. A function f : X → Y between uniform space is called uniformly continuous if for every entourage V in Y there exists an entourage U in X such that for every (x1, x2) in U we have (f(x1), f(x2)) in V.
In this setting, it is also true that uniformly continuous maps transform Cauchy sequences into Cauchy sequences and that continuous maps on compact uniform spaces are automatically uniformly continuous.
Each compact Hausdorff space possesses exactly one uniform structure compatible with the topology. A consequence is a generalisation of the Heine-Cantor theorem: each continuous function from a compact Hausdorff space to a uniform space is uniformly continuous.
References
- Nicolas Bourbaki, General Topology (Topologie Générale), ISBN 0-387-19374-X (Ch. 1–4): Chapter II is a comprehensive reference of uniform spaces
- Dieudonné, Jean (1960), Foundations of Modern Analysis, Academic Press
- Fitzpatrick, Patrick (2006), Advanced Calculus, Brooks/Cole
- Kelley, John L. (1955), General topology, Graduate Texts in Mathematics, Springer-Verlag, ISBN 0-387-80125-6
- Kudryavtsev, L.D. (2001), "Uniform continuity", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/U/u095220.htm
- Rudin, Walter (1976), Principles of Mathematical Analysis, New York: McGraw-Hill, ISBN 978-0-07-054235-8